Engineering Mathematics
Friday, April 4, 2014
Wednesday, July 24, 2013
Monday, February 11, 2013
Polylogarithm
Definition of Polylogarithm
Proof
(1)
(2)
summing (1) and (2)
(3)
(4)
(5)
using the definition of polylogarithm , the function equation is:
Tuesday, January 1, 2013
Saturday, December 1, 2012
Generating Function
GF.ID.1: Chebyshev polynomial
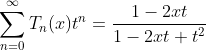 Given:
Given:
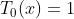
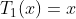
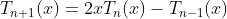
Expanding of Chebyshev polynomial as following:
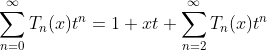
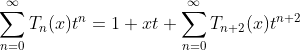
rewriting (1.c) as :
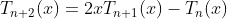
from (2.b) and (3)
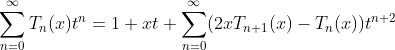
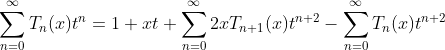

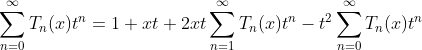
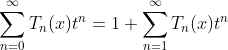
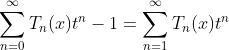
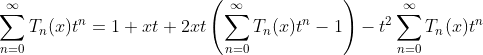
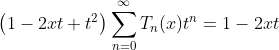
(1.a)
(1.b)
(1.c)
Expanding of Chebyshev polynomial as following:
(2.a)
(2.b)
rewriting (1.c) as :
(3)
from (2.b) and (3)
(4.a)
(4.b)
(4.c)
(4.d)
similar to (3) , Expanding of Chebyshev polynomial as following:
(5.a)
(5.b)
From (4.d) and (5.b) ,
(6.a)
(6.b)
rearranging (6.b)
Saturday, November 24, 2012
Dirichlet Series of Divisor Function
DF.ID.1: Dirichlet series of first and second order divisor function:
Euler product representation of Dirichlet series of divisor function:
(1.a)
(1.b)
(2.a)
(2.b)
according to
(3.a)
from (1.b) and (2.b):
(3.b)
The derivative of geometric series (GS.ID.1):
(4)
(5.a)
(5.b)
from ( 3.a) and (4) , the Dirichlet series of first order divisor function:
(6)
from (3.b) and (5.b) , the Dirichlet series of second order divisor function:
(7)
DF.ID.2: Dirichlet series of first order divisor function: of squared number
proof
(8)
(8.b)
(8.c)
given that :
(9)
The derivative of previous series:
(10)
(11)
from (8.c)(10) and (11),
(12)
(13)
DF.ID.3: Dirichlet series of sum of higher order divisor function:
Proof
(1)
(2)
(3)
(4)
(5)
(6)
(7)
replacing (7) in (6) gives:
(8)
(9)
(10)
(11)
(12)
(13)
Subscribe to:
Posts (Atom)